Luento 4 ti 18.9.

Tapahtumat:

[HAM]-kirjoja

KRE-kirjasta: 1.9 ss 52 - 59 . Lisäksi lineaarisia koskeva lause, jota ei ole tällä kohdalla KRE:ssä (vasta systeemien yhteydessä.) Tähän on prujut, sopiva kirja: [BdiP], (josta löytyy myös yleisen tapauksen tarkka todistuskin, sehän menee ohi kurssin).

AA-tehtävän ratkaisun olemassaolo- ja yksikäsitteisyys

Esimerkeissä olemme muuttujan erottelulla, integroivan tekijän menettelyllä ym. saaneet yleisen ratkaisun (paitsi jos implis. muoto) ja annettua alkuehtoa vastaavan 1-käsitteisen C:n, eli AA-tehtävillämme on ollut 1-käsitteinen ratkaisu. Poikkeuksena pisteet, joissa yhtälö ei ole määritelty (y' saisi arvon ääretön).

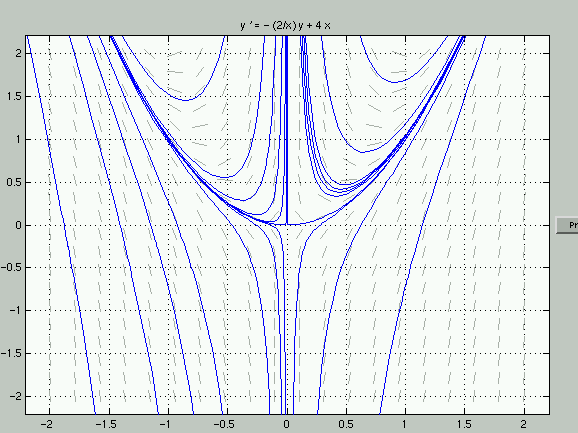
Yksikäsitteisyys näkyy geometrisesti niin, että ratkaisukäyräparven käyrät eivät leikkaa toisiaan.

Ratkaisun olemassaolo ja 1-käsitteisyys ovat perustuneet johdettuun ratkaisukaavaan. Tavallinen tilanne on kuitenkin se, ettei ratkaisukaavaa ole, mutta ratkaisun olemassaolo ja yksikäsitteisyys voidaan todistaa ja sitä voidaan numeerisesti approksimoida halutulla tarkkuudella.

Palataan ensin lineaariseen yhtälöön, jossa siis asiat selviävät kaavan avulla.

Lineaarinen yhtälö

(AA)  y' + p(x)y = r(x) , y(x₀) = y₀

Kysymykset

Onko olemassa
Voiko olla useita
Päteekö ratkaisu koko R:ssä vai jossain alkupisteen x₀ ystössä.

Saamme erittäin suurta tyydytystä tuottavan tuloksen:

Lause[LIN-E₁] Jos p ja r ovat jatkuvia välillä I=(a,b) ja a < x₀ < b , niin tehtävällä on 1-käs. ratk., joka on määritelty koko välillä I.

Tod: Voisimme sanoa, että olemme jo todistaneet tämän, mutta katsotaan nyt lähemmin.

Jatkuu käsin kirjoittaen ...

Yleinen (epälineaarinen) tapaus

Picard-Lindelöfin iteraatio

Tässä Maple- esimerkki