Z-muunnos ja differenssiyhtälöt
7.11.00
>
Z-muunnoksia ja käänteismuunnoksia
> restart:alias(Z=ztrans,IZ=invztrans);
Warning, the name changecoords has been redefined
![]()
> ztrans(1,n,z);
![]()
> ztrans(a^k,k,z):simplify(%);
![]()
> ztrans(k,k,z);
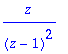
> Z(cos(k*alpha),k,z);Z(sin(k*alpha),k,z);
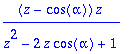
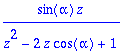
> seq(Z(x(k-j),k,z),j=1..4);
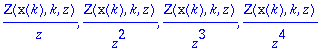
> seq(Z(x(k+j),k,z),j=1..3);
![]()
>
Käänteismuunnoksia
Z-käänteismuunnoksessa on annettu funktio z-> F(z) ja etsitään sen kertoimia, kun F(z) esitetään 1/z:n potenssien mukaan.
Jos F(1/z) on analyyttinen O:ssa, se voidaan kehittää potensssisarjaksi (1-käs.), jolloin F(z):lle saadaan sarjaesitys korvaamalla z 1/z:lla.
Esim:
> F:=z-> z/(z-2);G:=normal(F(1/z));
![]()
![]()
> subs(z=1/z,series(G,z=0,10));
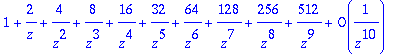
Maple osaa kehittää jopa äärettömyyspisteen ympäristössä, saadaan siis vielä yksinkertaisemmin:
> series(F(z),z=infinity,10);
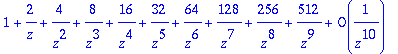
> IZ(F(z),z,k);
![]()
> F:=z-> z/((z-1)*(z-2));G:=normal(F(1/z));subs(z=1/z,series(G,z=0,10));
![]()
![]()
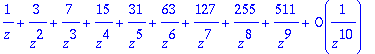
> IZ(F(z),z,k);seq(%,k=0..9);
![]()
![]()
> #convert(F(z),parfrac,z);map(IZ,[op(%)],z,k);
Exa 3.8:
> Y:=z/((z-1)*(z-2)):Yperz:=Y/z: Yperz:=convert(%,parfrac,z);
![]()
> Y:=expand(z*Yperz);IZ(Y,z,k);
![]()
![]()
Jos oltaisiin kehitetty suoraan jakamatta z:lla:
> Y:=convert(Y,parfrac,z);
![]()
> seq(1/(2*I*a)*a^k*(I^k-(-I)^k),k=0..10);seq(a^(k-1)*sin(k*Pi/2),k=0..10);
![]()
![]()
Differenssiyhtälöitä
Exa 3.15 s. 239
> dy:=y(k+2)+y(k+1)-2*y(k)=1;
![]()
> zdy:=ztrans(dy,k,z);
![]()
> Y:=solve(zdy,ztrans(y(k),k,z));
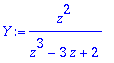
> y(0):=0:y(1):=1:
> Y;Y:=factor(%);
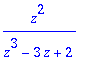
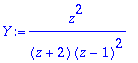
> Yperz:=convert(Y/z,parfrac,z);
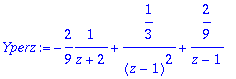
> Y:=expand(z*Yperz);
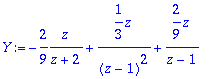
> invztrans(Y,z,k);
![]()
> yy:=unapply(%,k);
![]()
> subs(y=yy,dy);
![]()
> eval(%);
![]()
> simplify(%);
![]()
> plot([seq([k,yy(k)],k=0..8)]);
![[Maple Plot]](images/zmuunnos37.gif)
Voidaan ratkaista myös suoraan rsolve:lla (vrt. dsolve)
> restart:dy:=y(k+2)+y(k+1)-2*y(k)=1;
![]()
> rsolve({dy,y(0)=0,y(1)=1},y(k));yy:=unapply(%,k);
![]()
![]()
Toisaalta voidaan tietenkin muodostaa jonoa mielivalt. pitkälle suoraan rekursiokaavasta:
> %restart:
>
y(0):=0:y(1):=1:for k from 0 to 20 do
y(k+2):=1-y(k+1)+2*y(k): od:
> seq(y(k),k=0..20);seq(yy(k),k=0..20);
![]()
![]()
Exa 3.16
> restart:
>
dy:=8*y(k+2)-6*y(k+1)+y(k)=9;
zdy:=ztrans(dy,k,z);
Y:=solve(zdy,ztrans(y(k),k,z));
y(0):=1:y(1):=3/2:
Y;
![]()
![]()
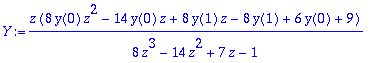
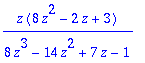
>
Yperz:=convert(Y/z,parfrac,z);
Y:=expand(z*Yperz);
invztrans(Y,z,k);
yy:=unapply(%,k);
subs(y=yy,dy);
eval(%);
simplify(%);
plot([seq([k,yy(k)],k=0..9)]);
![]()
![]()
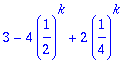
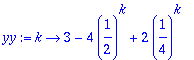
![]()
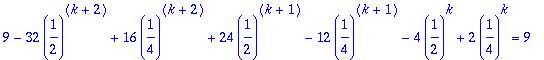
![]()
![[Maple Plot]](images/zmuunnos54.gif)
Exa 3.17 s. 242
>
restart:dy:=y(k+2)+2*y(k)=0;
zdy:=ztrans(dy,k,z);
Y:=solve(zdy,ztrans(y(k),k,z));
y(0):=1:y(1):=sqrt(2):
Y;
![]()
![]()
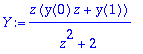
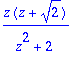
>
Yperz:=convert(Y/z,parfrac,z,{I,sqrt(2)});
>
Y:=expand(z*Yperz);
invztrans(Y,z,k);
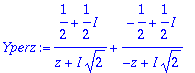
![]()
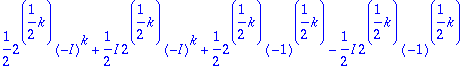
> yy:=evalc(%);
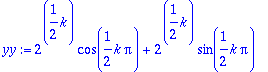
>
yy:=unapply(yy,k);
subs(y=yy,dy);
eval(%);
assume(k,integer):simplify(%);
plot([seq([k,yy(k)],k=0..9)]);
>
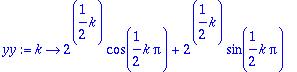
![]()
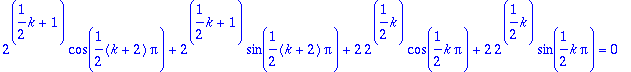
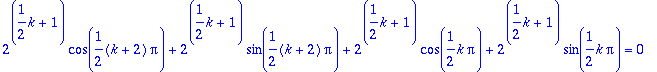
![]()
![[Maple Plot]](images/zmuunnos68.gif)
>
restart:dy:=y(k+2)+2*y(k)=0;
rsolve({dy,y(0)=1,y(1)=sqrt(2)},y(k));
![]()
![]()
> evalc(%);simplify(%,symbolic);
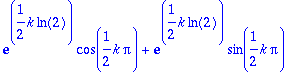
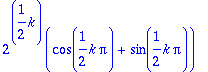
>
Stabiilisuus
> restart:alias(Z=ztrans,IZ=invztrans);
![]()
Katsotaan osamurtoja hieman tarkemmin
> F:=2*z^3+z^2+z+1:F:=F/(((z-I)*(z+I))^3);
> expand(denom(%));
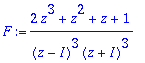
![]()
> convert(F,parfrac,z,I);
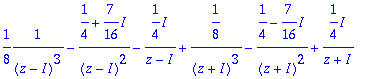
Määritellään kertomislauseeseen sopiva operaattori, annetaan z:n olla globaali.
> mdz:=F->(-z*diff(F,z));
![]()
> F:=z/(z-a):
> Fjono:=seq(simplify((mdz@@k)(F)),k=0..4);
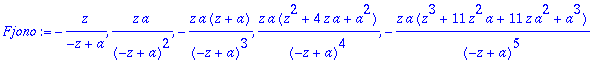
> Fjono[5];convert(%,parfrac,z);
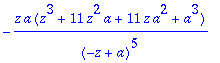
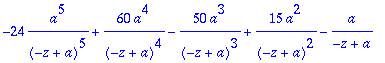
> ztrans(k^4*a^k,k,z);
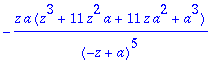
> IZ(1/(z-a)^4,z,k);
-6*a^k+11*a^k*k-6*a^k*k^2+a^k*k...](images/zmuunnos82.gif)
Nämä saadaan derivoinnista a:n suhteen, sittenkin helpommin kuin edellä kertomislausetta käyttäen. (Siinä menee
päättely vähän väärinpäin, vaikka antaa sekin hyvin uskoa asiaan.)
>
>
znavat:=proc(G,z)
# Muista kutsua näin:
# tulos:=proc(G,z): # numeroarvot: tulos[1]; # kuva: tulos[2];
local navat,kuva ;
navat:=[solve(denom(G)=0,z)];
kuva:=plots[display]([plot(zip((x,y)->[x,y],map(Re,navat),map(Im,navat)),style=point,symbol=circle),plot([cos(t),sin(t),t=0..2*Pi],scaling=constrained)]);
[navat,kuva];
end:
>
zstabiili:=proc(G,z)
max(op(map(abs,[fsolve(denom(G)=0,z,complex)])));
#fsolve(denom(G)=0,z,complex);
> end:
> G:=z^2/(z^3-3*z^2+2.5*z-1);
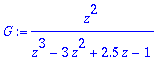
> zstabiili(G,z);
![]()
Warning, the name changecoords has been redefined
> tulos:=znavat(G,z):
> tulos[2];tulos[1];
![[Maple Plot]](images/zmuunnos85.gif)
![]()
> max(op(map(abs,tulos[1])));
![]()
Esim. 3.24, s. 256
> F:=1/(z^3+1/3*z^2-1/4*z-1/12);
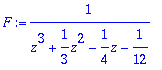
> tulos:=znavat(F,z):
> max(op(map(abs,tulos[1])));
![]()
> tulos[2];tulos[1];
![[Maple Plot]](images/zmuunnos90.gif)
![]()
> zstabiili(F,z);
![]()
Exa 3.25
> G:=1/(z^3-3*z^2-1/4*z+3/4);
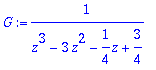
> tieto:=znavat(G,z):
> tieto[2];tieto[1];
![[Maple Plot]](images/zmuunnos94.gif)
![]()
>
Konvoluutio
> zconv:=(x,y,k)->sum(x(j)*y(k-j),j=0..k);
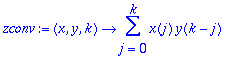
>