varaht01.html

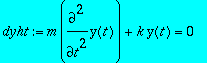
Värähtelyliike

2.10.01 HA

Vapaa vaimentamaton , eli harmoninen värähtely

> restart: dyht:=m*diff(y(t),t,t)+k*y(t)=0;

Warning, the name changecoords has been redefined

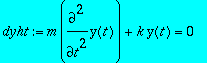
> parametrit:={k=2,m=1}: assign(parametrit): k:='k': m:='m': # Mutta vapautetaan takaisin.

> w0yht:=w0=sqrt(k/m): T:=2*Pi/w0: f0:=1/T: # w0yhtälö sijoitukseksi: assign(w0yht):

Yrite:

> y:=A*cos(w0*t)+B*sin(w0*t); dy:=diff(y,t); d2x:=diff(dy,t);

> vasenp:=m*d2x+k*y;

> assign(w0yht): w0;

> simplify(vasenp);

Yritteemme siis toimii.

Alkuehdot:: x(0)=1, x'(0)=0, vaikkapa:

> map(eval,{subs(t=0,y)=1,subs(t=0,dy)=0}): solve(%,{A,B});assign(%):y;

> assign(parametrit):plot(y,t=0..2*Pi);

Tämän mallin pohjalta on helppo tehdä erilaisia tapauksia. Muutellaan vain parametrejä ja alkuehtoja.

Lisäksi amplitudi ja vaihekulma, eli . Jätetään oppilaille.

Vrt. Matlab: varahtely.m Oppilaat: Tee BdiP esim. vihko s. -28-

Vaimennettu, tapaus I, ylivaimennus (vapaa, HY)

> restart:

Warning, the name changecoords has been redefined

> karpol:=lambda^2+c/m*lambda+k/m;

> Lambda:=solve(karpol=0,lambda);

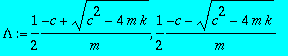
> diskr:=c^2-4*m*k:

> y:=C1*exp(Lambda[1]*t)+C2*exp(Lambda[2]*t);

>

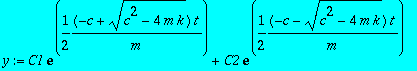
Kriittinen vaimennus, LRT ratkaisun etsintä

Alkeellinen perustapa:

> restart:y:=t*exp(lambda*t);dy:=diff(y,t);d2y:=diff(dy,t);

Warning, the name changecoords has been redefined

> m*d2y+c*dy+k*y;coeff(%,exp(lambda*t));collect(%,t);kert:=coeffs(%,t);

> yhtsys:={kert[1]=0,kert[2]=0};solve({kert[1]=0},{lambda});subs(%,kert[2]=0);map(expand,4*m*%);

$yhtsys := {2*m*lambda+c = 0, m*lambda^2+c*lambda+k ...$

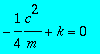
Sama ns. "elegantisti". Määritellään diffyhtälö niinkuin se yleensäkin Maplessa tehdään:

> restart:dyht:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=0;

Warning, the name changecoords has been redefined

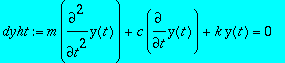
> yf:=t->t*exp(lambda*t);

> vp:=lhs(dyht);

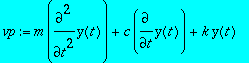
> eval(subs(y(t)=yf(t),vp)):collect(%,exp(lambda*t));

> coeff(%,exp(lambda*t));

> expand(%);

> p1:=collect(%,t);

> yht:={coeff(p1,t)=0,coeff(p1,t,0)=0};

$yht := {m*lambda^2+c*lambda+k = 0, 2*m*lambda+c = 0...$

Ratkaisemme :n jälkimmäisestä.

> Lambda:=solve(yht[2],lambda);

Sijoitamme edelliseen, saamme kriittisen vaimennuksen ehdon, joka oletuksemme mukaan on voimassa.

> subs(lambda=Lambda,yht[1]);

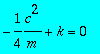
> map(expand,4*m*%);

Katsotaan vielä kerrotussa muodossa. Yritteemme toteuttaa siis diffyhtälön ja meillä on käsissämme 2 LRT ratkaisua.

Exa 2, KRE s. 90

> restart:

Warning, the name changecoords has been redefined

> dyht:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=0;
karyht:=m*lambda^2+c*lambda+k=0;diskr:=c^2-4*m*k;

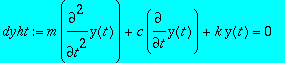
> m:=9.082:k:=890:

> karyht;

>

Tapaus I, ylivaimennus

> c:=200:

> karyht;

> Lambda:=solve(karyht,lambda);

> y:=C1*exp(Lambda[1]*t)+C2*exp(Lambda[2]*t);

> AE:=map(eval,{subs(t=0,y)=0.15,subs(t=0,diff(y,t))=0});

> solve(AE,{C1,C2});

> Y:=subs(%,y);

> plot(Y,t=0..1);

>

Tapaus II, kriittinen vaimennus

> c:=179.81078: diskr;

> karyht;

> Lambda:=solve(karyht,lambda);

> digits:=50;Lambda:=solve(karyht,lambda);

Kriittinen vaimennus on tietysti ideaalitapaus, käytännön laskuissa tulee pieni imag. termi tai sitten pieni ero reaalisten lambdojen välillä.

Tässä saadaan hyvä approksimaatio jättämällä pienet imaginaariosat pois.

> lambda:=Re(Lambda[1]);

> y:=(C1+C2*t)*exp(lambda*t);

> AE:=subs(t=0,y)=0.15,subs(t=0,diff(y,t))=0;solve({AE},{C1,C2});Y:=subs(%,y);plot(Y,t=0..1);

Kuva näyttää jokseenkin samanlaiselta kuin ylivaimennetussa tap.

Tapaus III, alivaimennus

> lambda:='lambda':

> c:=100:

> karyht;Lambda:=solve(karyht,lambda);

> lambda:=Lambda[1]:alpha:=-Re(lambda);w1:=abs(Im(lambda));

w1 on KRE:n omega*

> y:=exp(-alpha*t)*(C1*cos(w1*t)+C2*sin(w1*t));

> AE:=subs(t=0,y)=0.15,subs(t=0,diff(y,t))=0;solve({AE},{C1,C2});Y:=subs(%,y);

> plots[display](array([[plot(Y,t=0..4),plot(Y,t=0.5..3),plot(Y,t=1..3)]]));

> plot(Y,t=0..4,axes=boxed);

Tehtävän Matlab-käsittelyä varten tarvittava Maple-osuus:

> restart:y:=exp(alpha*t)*(C1*cos(w1*t)+C2*sin(w1*t));

Warning, the name changecoords has been redefined

> dy:=diff(y,t);

> dy:=collect(dy,{cos(w1*t),sin(w1*t),exp(-alpha*t)}):lprint(%);

(alpha*exp(alpha*t)*C1+exp(alpha*t)*C2*w1)*cos(w1*t)+(alpha*exp(alpha*t)*C2-exp(alpha*t)*C1*w1)*sin(w1*t)

> eval(subs(t=0,y))=y0,eval(subs(t=0,dy))=v0;

> solve({%},{C1,C2}):lprint(%);

{C2 = (-alpha*y0+v0)/w1, C1 = y0}

>

Pakotettu värähtely, EHY

> restart:dyht:=m*diff(x(t),t,t)+c*diff(x(t),t)+k*x(t)=F0*cos(w*t);

Warning, the name changecoords has been redefined

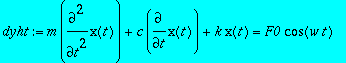
Käytetään :n sijasta :tä, koska omega0 ei ole hauska. Voisimme johtaa kaavat Maple-avusteisesti, mutta yhtä hyvin voimme johtaa ne kynä/paperi/oppikirja-tekniikalla siltä osin, kuin se ei ole liian työlästä.

Tapaus 1. Vaimentamaton pakkovärähtely

>

Ei resonanssi , eli

> yh:=t->C*cos(w0*t-delta); # Operoimme funktioilla (eikä lausekkeilla).

> w0=sqrt(k/m); # Emme tee sijoitusta, muistutamme vain

> yp:=F0/(m*(w0^2-w^2))*cos(w*t);

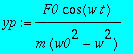
> yp:=t->kerroin*F0*cos(w*t);

> kerroin:=1/(m*(w0^2-w^2));

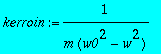
> #kerroin:=1/(k*(1-(w/w0)^2)); # Kumpi vain, molemmathan ovat samoja.

> yp(t);

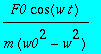
> y:=yh+yp; # Funkiot lasketaan yhteen.

> y(t);

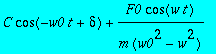
> a0:=F0/k*rho;

> rho:=1/(1-(w/w0)^2);

>

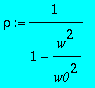
Resonanssi,

> restart:

Warning, the name changecoords has been redefined

> yp:=t*(a*cos(w0*t)+b*sin(w0*t));

> dyp:=diff(yp,t):d2xp:=diff(dxp,t):

> m*d2xp+k*xp=F0*cos(w0*t):collect(%,{t,sin(w0*t),cos(w0*t)});#kert:=coeffs(%,t);

> -m*a*w0^2+k*a+2*m*b*w0=F0,-m*b*w0^2+k*b=0,2*m*a*w0=0;

> solve({-m*a*w0^2+k*a+2*m*b*w0=F0,2*m*a*w0=0},{a,b});

> assign(%);

> yp;

> m:=1:F0:=1:w0:=10:

> plot(yp,t=0..30);

>

Huojunta, beats

>

Tapaus 2. Vaimennettu pakkovärähtely

> restart:W0:=w0=sqrt(k/m):assign(W0): w0:='w0':

Warning, the name changecoords has been redefined

> Aab:={a=F0*m*(w0^2-w^2)/detA,b=F0*w*c/detA,detA=m^2*(w0^2-w^2)^2+w^2*c^2};

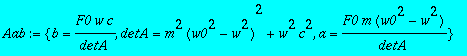
$Aab := {b = F0*w*c/detA, detA = m^2*(w0^2-w^2)^2+w^...$

> assign(Aab);

> detA:='detA':a:='a':b:='b':

> yht2:={alpha=c/(2*m),diskr=c^2-4*m*k,w1=sqrt(-diskr)/(2*m),beta=I*w1};

$yht2 := {alpha = 1/2*c/m, diskr = c^2-4*m*k, beta =...$

> assign(yht2):

> alpha:='alpha':w1:='w1': beta:='beta':

> a:='a': b:='b':#beta;

> yh:=exp(-alpha*t)*(A*cos(w1*t)+B*sin(w1*t));

> yp:=a*cos(w*t)+b*sin(w*t);

> ypp:=C1*cos(w*t-delta);

> ypp:=expand(ypp);

> coeff(yp,cos(w*t))=coeff(ypp,cos(w*t)),coeff(yp,sin(w*t))=coeff(ypp,sin(w*t));

> %solve({%},{C1,delta}):

> %map(allvalues,%):

> C1:=sqrt(a^2+b^2);#delta:=arctan(b,a);

> assign(Aab);

> C1;

>

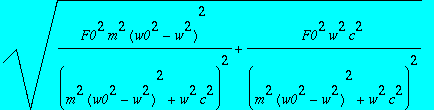
> C1:=simplify(%,symbolic);

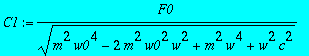
> #C1:=F0/(sqrt(factor(m^2*w0^4-2*m^2*w0^2*w^2+m^2*w^4+w^2*c^2)));

> m^2*(w0^2-w^2)^2+w^2*c^2;

> expand(%);

> C1:=F0/sqrt(m^2*(w0^2-w^2)^2+w^2*c^2);

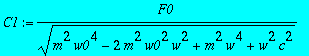
> b;

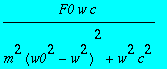
> a;

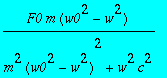
> b/a;

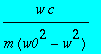
> eta:=arctan(w*c,(m*(w0^2-w^2)));

>

Ratkaistaan konkreettinen esim. enemmän Maple-avusteisesti

> restart:

Warning, the name changecoords has been redefined

> EHY:=m*diff(y(t),t,t)+c*diff(y(t),t)+k*y(t)=r(t):

m=massa, c=vaimennuskerroin, k=jousivakio, r(t)=ulkoinen voima.

> HY:=lhs(EHY)=0:HY:=subs(m=1,c=4,k=24,r(t)=10*cos(omega*t),HY);

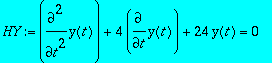
> diskr:=c^2-4*m*k: subs(m=1,c=4,k=24,diskr);

Siis alivaimennus, joten värähtelyä on luvassa.

Ajatellaan, että HY on jo selkäytimessä, annetaan siten rutiinitehtävä Maplen dsolve :lle .

> dsolve(HY,y(t));

> yh:=rhs(%);

> parametrit:={m=1,c=4,k=24}:assign(parametrit):

> omega[1]=sqrt(-'diskr')/(2*'m'),omega[1]=sqrt(-diskr)/(2*m);
alpha='c'/(2*'m'),alpha=c/(2*m);

>

Pitipä tarkistaa, että Maple laski oikein, kyllä vaan!

Suoritetaan EHY-yritelasku peruskäyttötavalla vetoamatta Maplen diffyhtälörakenteeseen.

Yrite:

> xp:=a*cos(omega*t)+b*sin(omega*t): dxp:=diff(xp,t):d2xp:=diff(dx,t):vp:=m*d2xp+c*dxp+k*xp;
oip:=10*cos(omega*t);abyht:={coeff(vp,cos(omega*t))=coeff(oip,cos(omega*t)),coeff(vp,sin(omega*t))=0};

>

> ab:=solve(abyht,{a,b});

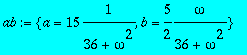
$ab := {a = 15*1/(36+omega^2), b = 5/2*omega/(36+ome...$

> assign(ab):

> C12:=a^2+b^2;

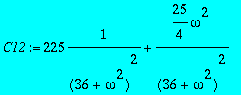
> C12:=normal(C12);

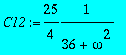
Max-amplitudi saadaan, kun =0, joten tässä ei resonanssityylistä maksimia synny (vaimennus on suuri).

Seuraava lasku on siten tarpeeton, mutta laitetaan se mukaan, tässähän on helppo vaihdella parametrejä.

> nim:=denom(%);

> solve(diff(nim,omega)=0,omega);

> C1:=sqrt(C12);

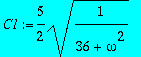
> plot(C1,omega=0..6);

> kuva6:=plot(subs(omega=6,xp),t=0..5,color=red):kuva4:=plot(subs(omega=4,xp),t=0..5,color=blue):kuva1:=plot(subs(omega=1,xp),t=0..5,color=gold):

> plots[display]([kuva1,kuva4,kuva6]);

> w1;

> C1;

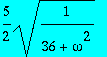
> evalf(subs(omega=4,C1));evalf(subs(omega=6,C1));evalf(subs(omega=1,C1));

>

Yleiset lineaariset yhtälöt