V3, välikoe 3

Joulukuu 2001, HA

1.

> restart:with(plots):
read("/home/apiola/opetus/peruskurssi/v2-3/maple/fourier.mpl"):

Warning, the name changecoords has been redefined

> f:=t->t:

> fj2:=JJ(f,-1..1);plot(fj2,-3..3);

Funktio on pariton, joten kerrottaessa cosinilla, tulee parillista ja integroitaessa yli välin [-1,1] saadaan 0.

Siten tarvitsee laskea vain b-kertoimet, niiden integroitavat ovat parillisia, joten viodaan integroida

yli välin [0,1] ja kertoa tulos kahdella. (Säästää vähän laskutyötä.)

>

> bn:=2*(2/T)*Int(f(t)*sin(n*omega*t),t=0..T/2);

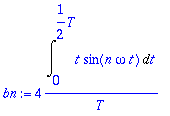
> T:=2: omega:=2*Pi/T;

> bn;

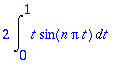
Tämä on lyhyt osittaisintegrointitehtävä, annan tässä Maplen hoitaa homman:

> bn:=value(bn);bn:=trigsiev(bn,n);

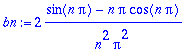
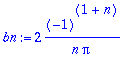
> sarja:=Sum(bn*sin(n*omega*t),n=1..infinity);

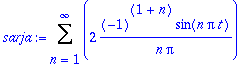
Koetehtävä on valmis, mutta annetaan maplen vielä piirtää (ei sitä voi estääkään).

> osasumma:=(t,N)->sum(bn*sin(n*omega*t),n=1..N):

> plot([fj2(x),seq(osasumma(x,N),N=1..10)],x=-3..3);

> plot([fj2(x),seq(osasumma(x,N),N=1..3),osasumma(x,30)],x=-3..3);

2.

a)

> restart:

Warning, the name changecoords has been redefined

Kohta 1: x=(1,1,1,...).

> Sum(1*z^(-k),k=0..infinity): %=value(%);

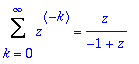
Tämä tulee suoraan geometrisen sarjan summan kaavasta (q=1/z) ja edellyttää: | z | > 1.

Kohta 2: 2^k = 1*2^k, joten vasemmanpuolisen kertosäännön mukaan (a=2):

> Z(1*2^k)=X(2^(-1)*z);

missä

> X:=z->z/(-1+z);

> X(1/2*z): X2:=normal(%);

Kohta 3)

Oikeanpuolinen kertosääntö (n=1) antaa:

> Z(k*2^k)=normal(-z*diff(X2,z));

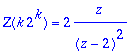
Nämä ovat kaikki lyhyitä käsinlaskuja.

b)

> restart: alias(Z=ztrans,IZ=invztrans);

Warning, the name changecoords has been redefined

> dify:=y(k+2)-5*y(k+1)+6*y(k)=delta(k);Zdify:=Z(dify,k,z):Zdify:=subs(y(0)=0,y(1)=0,%);

> Zdify:=subs(Z(delta(k),k,z)=1,Zdify);

> Y:=solve(%,Z(y(k),k,z));
Y:=convert(%,parfrac,z);

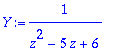
Tähän saakka kaikki on hyvin mekaanista. Miten nämä käämteismuunnetaan?

Olkoon

> Y1:=1/(z-3); Y1:=z*Y1/zeta; # Lavennuksen onnistumiseksi merkitään z:aa myös zeta:lla.

Vasen siirtosääntö (k0=1) antaa:

> y1:=0,seq(3^(k-1),k=1..10);

Aivan samoin toinen:

> y2:=0,seq(2^(k-1),k=1..10);

Tietysti kyseessä on äärettömät jonot eikä 10:n pituiset.

Käänteismuunnos, eli ratkaisu on siis näiden erotus, eli:

> y:=seq(y1[k]-y2[k],k=1..10);

Toisn sanoen:

> y:='y':

> y(0)=0; y(k)=3^(k-1)-2^(k-1);

Vaihtoehtoisesti on kenties vielä helpompi laskea suoraan Z-muunnoksen määritelmästä, niin että itse asiassa johdetaan samalla siirtosääntö tässä erikoistapauksessa.

(Siirtosäännön johtaminen on ehkä helpompaa kuin sen soveltaminen.)

Tarkistetaan:

> yy:=IZ(Y,z,k);seq(yy,k=0..9);

c)

Ainoa mahdollinen vaikeus on siinä, että tämä on liian helppo. Laitoin tehtävän johdatelevasti muotoon "kirjoita" ...

> X:=(3*z+z^2+5*z^5)/z^5; X:=expand(%);

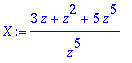
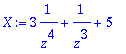
Funktio X(z) on nyt valmiiksi kehitettynä (1/z):n potenssien mukaan. Sarjakehitelmässä sattuu olemaan vain äärellinen määrä termejä. Kääntyeismuunnos on sitem:

> [5,0,0,1,3,0,0,0,0,0,nollatjatkuvat];

> IZ(X,z,k);

Maplen käänteismuuntaja on siis samaa mieltä.

3.

(a)

Tämä on helppo laskea suoraan ehdollisen todennäköisyyden avulla:

Olkoon A="1. nostolla punainen" ja B="2. nostolla punainen".

P("molemmat punaisia") = P(A ja B) = P(A)*P(B | A)

P(A) = 5/20 = 1/4, P(B | A) = 4/19 , joten

> tod(a) := 1/19;

(b)

> restart: with(combinat):alias(B=binomial):B(4,2); # Binomikerroin

Warning, the name changecoords has been redefined

Warning, the protected name Chi has been redefined and unprotected

Merkitään sinistä S:llä ja ei-sinistä C:llä (Co-sini).

> [S,S,S,S,S,S,C,C,C,C,C,C,C,C,C,C,C,C,C,C];

Otoskoko: n=3, N=20 , M = #S = 6, #C = N-M = 14.

Kaikkien otosten lkm = B(N,n) = B(20,3).

Sinisiä voidaan valita 2 kpl B(M,2) = B(6,2) :lla tavalla. Kutakin tapaa kohti voidaan "cosinisiä" valita 1 kpl 14:lla tavalla. Suotuisia tapauksia siis

> suotuisat:=14*B(6,2); kaikki:=B(20,3);

> tod(b):=suotuisat/kaikki;evalf(%);

4.

> restart:

Warning, the name changecoords has been redefined

(a)

Osoitetaan, että .

> Phi(-x)=Int(phi(t),t=-infinity..-x);

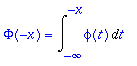
Suoritetaan muutujanvaihto , jolloin

> Phi(-x)=-Int(phi(-s),t=infinity..x);

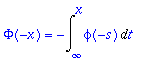
Vaihdetaan rajat, muutetaan merkki ja käytetään :n parillisuutta, jolloin saadaan:

> Phi(-x)=Int(phi(s),t=x..infinity);

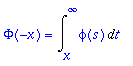
Siispä:

> Phi(x)+Phi(-x) = Int(phi(t),t = -infinity .. x)+Int(phi(s),t = x .. infinity);

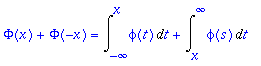
Siispä:

(b)

Tässä käytetään Maplea ensisijassa älykkäänä matemaattisena tekstinkäsittelysysteeminä.

> restart:

Warning, the name changecoords has been redefined

> erfyht:=erf(x) = 2/sqrt(Pi) * Int(exp(-t^2), t=0..x); # Olen kieltänyt nämä, jos käytetään sijoitusmerkkiä :=

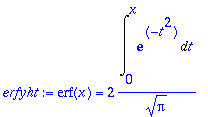
Olkoon taas normeeratun normaalijakauman tiheysfunktio.

> Phi(x)=(Int(phi(t),t=-infinity..0)+Int(phi(t),t=0..x));

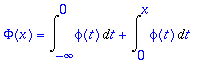
Edellinen integraali on (jälleen parillisuuden takia) = 1/2.

> phi:=x->1/sqrt(2*Pi)*exp(-t^2/2);

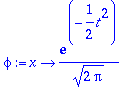
> Phi(x)=1/2+Int(phi(t),t=0..x);

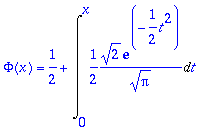
Muuttujanvaihto:

> sij:=t=sqrt(2)*u,dt=diff(sqrt(2)*u,u)*du;

> subs(sij,1/2*sqrt(2)*exp(-1/2*t^2)/(sqrt(Pi))*dt);

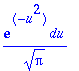
> Phi(x) = 1/2+Int(%,u = 0 .. x/sqrt(2));

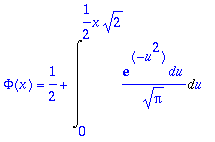
Lavennetaan integraalitermi 2:lla, jolloin saadaan:

> Phi(x) = 1/2+kaksi*Int(exp(-u^2)*du/(sqrt(Pi)),u = 0 .. 1/2*x*sqrt(2))/2;

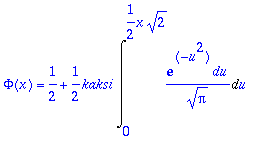
> erfyht;

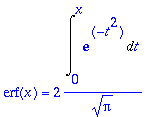
Siispä:

> Phi(x)=1/2*(1+erf(x/sqrt(2)));

(c)

> restart:

Warning, the name changecoords has been redefined

> F:=x->Phi((x-mu)/sigma);

Hyväksymisväli on

Normeeratun kertymäfunktion avulla ilmaistuna:

> F(mu+c)-F(mu-c);

(a)-kohdan mukaan sievenee muotoon:

> Phyv:=subs(Phi(-c/sigma)=1-Phi(c/sigma),%);

Lausutaan erf: n avulla (Kohta (b)):

> Phi:=x->1/2+1/2*erf(x/sqrt(2));

> Phyv;

Hyväksyttävien osuus 0.96, joten ratkaistavana on yhtälö

> Phyv=0.96;

Tehtäväpaperissa annettiin:

> solve(erf(y)=0.96,y);

Käsin/laskimella jää ratkaistavaksi yhttälö:

> (1/2*c*sqrt(2)/sigma)=1.452219782;

Siitä saadaan:

> solve(%,c); subs(sigma=0.02,%);

Vastaus (c)-kohtaan: c=0.04107

Odotusarvo ei vaikuta asiaan.

Maplella oltaisiin tietysti voitu jättää yksi vaihe väliin:

> Phyv=0.96;subs(sigma=0.02,%);solve(%,c);