![[Up]](/gadgets/trup.gif)
(1) f(x) = 0
INPUT f,a,b,tol,maxiter
1. i:=1
2. WHILE i <= maxiter DO
c:=(a+b)/2
IF (f(c)=0 OR (b-a)/2 < tol) RETURN(c) FI
i:=i+1
IF f(a)*f(c) > 0, a:=c ELSE b:=c # Tässä on asian ydin.
ENDDO (OD)
PRINT("Toleranssia ei saavuteta ",maxiter," "iteraatiolla")
END
Kuten heti nähdään, bisektioalgoritmin virhe n:nnen askeleen jälkeen
on korkeintaan
(b-a)/2n
Huom:
Alkupiste x0 .
xn+1 = g(xn), n= 0,1,2,...
Eräs päämäärä iteroinnille on löytää g:n kiintopiste, ts. piste x,
jolle
g(x) = x .
Kiintopiste on toisin sanoen piste, jonka iteroitava funktio pitää paikallaan.
> for k from 0 to 5 do x[k+1]:=g(x[k]) od:
> seq(x[k],k=0..5);
x[0], g(x[0]), g(g(x[0])), g(g(g(x[0]))), g(g(g(g(x[0])))),
g(g(g(g(g(x[0])))))
Maplessa on myös funktioiden yhdistämisoperaattori @, ja iterointi voidaan
toteuttaa elegantisi tyyliin g@@n . Edellinen voidaan siten tehdä myös
näin:
seq((g@@k)(x[0]),k=0..5);
(2) (3) (4) (5)
x[0], g(x[0]), (g )(x[0]), (g )(x[0]), (g )(x[0]), (g )(x[0])
Tällaisessa kumulatiivisessa iteroinnissa jälkimmäinen, vaikkakin elegantti,
on tehottomampi, koska jokainen iterointi aloitetaan aina alusta.
Kolme käytännön neuvoa (vanhan ja viisaan):
Toinen hauska tapa on ns. "cobweb"-piirros, jossa piirretään samaan koordinaatistoon funktion kuvaaja sekä suora y=x. Näiden leikkauspisteitä haetaan (nehän ovat juuri kiintopisteitä).
Lähdetään jostain x0:sta lasketaan y0=f(x0). Tämä on seuraava x1, joten graafisesti se saadaan menemällä vaakajanaa y=y0 suoralle y=x. Sitten vain jatketaan. Tässä Cobweb-opetusta (Univ. of Montana)
x2 - 3x +1 =0
Valitaan iterointifunktioksi
g(x)=(1/3)(x2 +1)
Maplessa:
> g:=x->(1/3)*(x^2+1);
2
g := x -> 1/3 x + 1/3
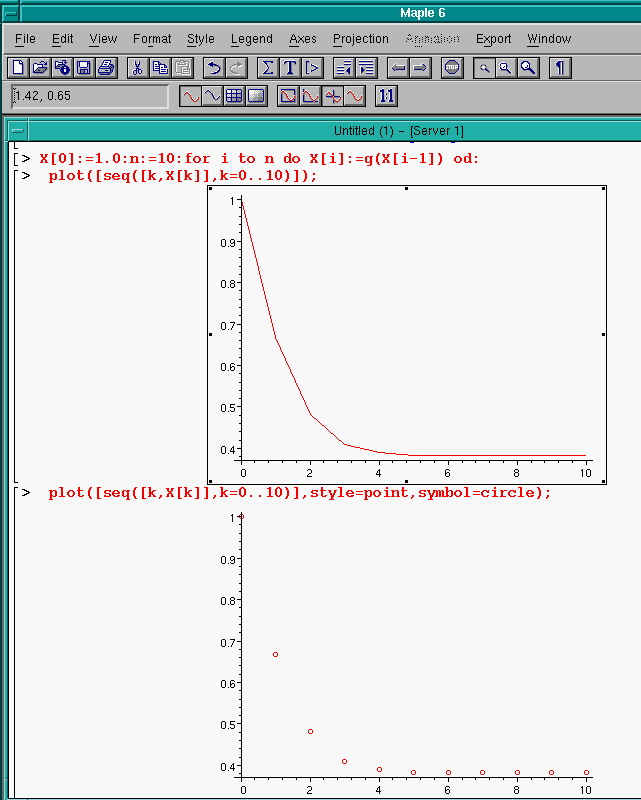
> X[0]:=1.0:n:=10:for i to n do X[i]:=g(X[i-1]) od:
> seq(X[k],k=0..10);
1.0, .6666666666, .4814814814, .4106081389, .3895330145, .3839119898,
.3824628053, .3820925991, .3819982514, .3819742213, .3819681019
Aikasarja
> plot([seq([k,X[k]],k=0..10)]);STYLE-valikosta voidaan valita yhdistysjanat mukaan (oletus) tai pois (style=point), mikä voidaan antaa myös komentona, kuten alla.

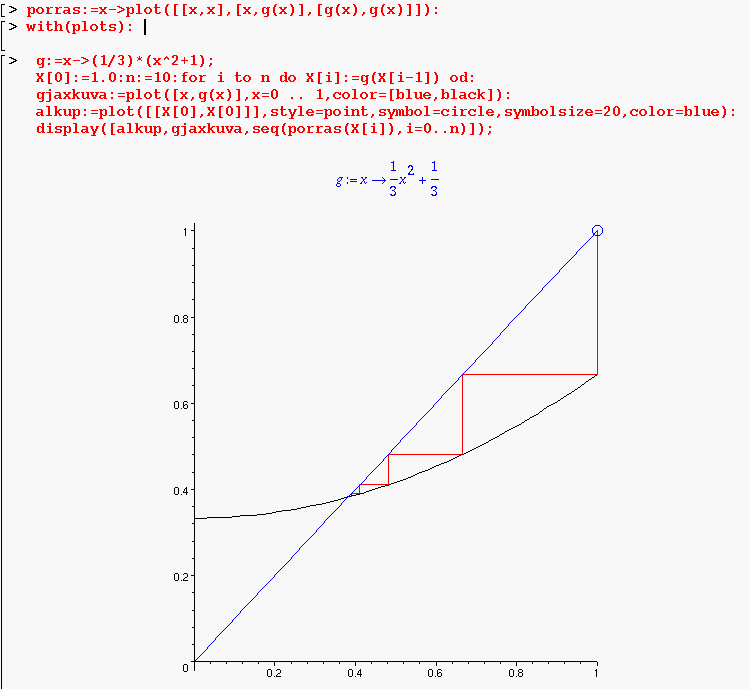
Cobweb Elegantti Maple-toteutus saadaan määrittelemällä grafiikka-arvoinen funktio porras
porras:=x->plot([[x,x],[x,g(x)],[g(x),g(x)]]):Tämä funktio liittää argumenttina annettuun x:ään porrasviivakuvan. (Funktion argumenttina on reaalilukua edustava symboli x ja arvona Maplen kuvatietorakenne.) Tässä g on globaali symboli, voitaisiin ottaa toiseksi argumentiksi, mutta tällä tavalla menee vaivattomammin, kun muistetaan aina nimetä iteroitava funktio g:ksi.
with(plots): g:=x->(1/3)*(x^2+1); X[0]:=1.0:n:=10:for i to n do X[i]:=g(X[i-1]) od: gjaxkuva:=plot([x,g(x)],x=0 .. 1,color=[blue,black]): alkup:=plot([[X[0],X[0]]],style=point,symbol=circle,symbolsize=20,color=blue): display([alkup,gjaxkuva,seq(porras(X[i]),i=0..n)]);
> X[10],g(X[10]);
.3819681019, .3819665436
Viiden numeron tarkkuudella olemme kiintopisteessä.
1. havainto
Jos g on jatkuva ja jos tiedämme, että kp-iteraatio xn+1 = g(xn) suppenee, sanokaamme c:tä kohti, niin c on g:n kiintopiste. Tämä seuraa heti jatkuvuudesta:
xn+1=g(xn),Vasen puoli suppenee kohti c:tä ja oikea g:n jatkuvuuden takia kohti g(c):tä.
Tyypillinen klassinen "peruskurssiteknikka" rekursiivisesti määritellyn jonon raja-arvon laskemiseen on tällainen:
Otamme samantien hieman tarkemmin kuin KRE-kirjassa, koska luonnollisista oletuksista saamme suorastaan ilmaiseksi myös kiintopisteen olemassaolo- ja yksikäsitteisyysjohtopäätöksen. (KRE-kirjassa oletetaan kiintopisteen olemassaolo.)
Tässä Latex-lähdekoodi. Taidanpa antaa Latex-kehyksen, jolla itsekukin voi ajaa nämä kauniisti. Toisaalta tätähän lukee kuin avointa kirjaa.
{\bf Kiintopistelause }
Olkoon $g\in C[a,b]$ ja $g(x)\in [a,b] \ \ \forall x\in [a,b]$, ts. $g$ kuvaa välin
$[a,b]$ sille itselleen. Tällöin $g$:llä on kiintopiste välillä $[a,b]$.
Jos lisäksi oletetaan, että $g$ on derivoituva ja
$$|g'(x)| \leq k \ \ \forall x\in [a,b],$$
missä $k<1$, niin kiintopiste on yksikäsitteinen ja iteraatiojono
$x_n=g(x_{n-1}), n=0,1,\ldots$ suppenee mielivaltaisella alkupisteen $x_0$
valinnalla, $x_0\in [a,b]. $
Tod:
(1) Olemassolo hoituu
{\em Bolzanon lauseella}
Jos $g(a)=a$ tai $g(b)=b$, on kiintopiste
löytynyt.
Oletetaan, että näin ei ole, eli $g(a)\ne a$ ja $g(b)\ne b$. Oletuksemme mukaan
täytyy silloin olla $g(a)>a$ ja $g(b)0$ ja $g(b)<0$,
joten
{\em Bolzano} $\implies \exists p\in [a,b]$ siten, että $h(p)=0$, eli
$f(p)=p$.
(2) Yksikäsitteisyys seuraa suoraan väliarvolauseesta:
Jos olisi kaksi eri kiintopistettä $p\ne q$ välillä $[a,b]$, niin
$$p-q=f(p)-f(q)=f'(\xi)(p-q),$$ joten saataisiin ristiriitainen epäyhtälö
$$|p-q| < k |p-q| < |p-q| .$$
(3) Suppeneminen seuraa epäyhtälöketjusta:
$|x_n -p| = |g(x_{n-1}) -g(p)| = |g'(\xi)||x_{n-1}-p| \leq k|x_{n-1}-p|
\leq \ldots \leq k^n |x_0-p|.$
Koska $0 < k < 1$, niin $\lim_{n\to\infty}x_n = p .$
Vrt. myös [HAM] ss. 120-121
> restart: > N:=x->evalf(x-f(x)/D(f)(x)); > Nsymb:=x->x-f(x)/D(f)(x);Käyttöesimerkki> f:=x->cos(x)-x; > Nsymb(x); > seq((N@@n)(1.0),n=0..5); > Matrix([seq([n,(N@@n)(1.0)],n=0..5)]); # Kätevä tapa taulukoida.
alaind: yläind: R^n Rn